Answered By : Mowji
I assume that we start labeling heights from $0$. Actually your approach is right. You must consider the left-side (or right-side) sub-tree with the least possible amount of nodes and the right-side (or left-side) sub-tree with the most possible amount of nodes, and both sub-trees must be AVL trees too. For this purpose, we fix the height of left-side sub-tree to $h-2$ (doing so, the bottommost node of this sub-tree would be at height $h-1$ of the main tree) and we fix the height of right-side sub-tree to $h-1$. Now, we should answer following questions:
- What is the minimum number of nodes in an AVL tree of height $h-2$?
- What is the maximum number of nodes in an AVL tree of height $h-1$?
Answer to question 1: By recursions and assuming that $n(h)$ is the minimum number of nodes of an AVL tree of height $h$ we can easily get: $$ begin{array}{rl} n(h) &=& n(h-1)+n(h-2)+1 n(1)&=&2 n(0)&=&1 end{array} $$ Answer to question 2: In this case, we’re dealing with a perfect tree (which is an AVL tree too) and we must find the number of nodes in a perfect tree of height $h-1$. So, the answer to your question would be: $$ 2^h – 1 – n(h-2) $$ As an example, if $h=2$, this formula returns $2$, which is not the value you have got, and I think that’s because you start labeling heights from $1$.
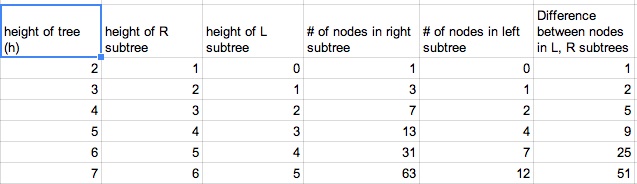
Problem Detail: Question: If an AVL tree has height h (assume h ≥ 2), what is the maximum possible difference between the number of nodes in its two subtrees? Prove your answer. Your answer should not use big-Oh or big-Theta. I drew six trees and drew the max number of nodes I could on one tree and the min number of nodes on the other subtree while keeping it an AVL tree. Here is table with the information for number of minimum nodes in left subtree, max number of nodes in right subtree and difference between the number of nodes between the two trees: 
But I simply cannot figure out a pattern for the maximum possible difference between the number of nodes in the two subtrees. My current guess is that the max possible difference between the two number of nodes is 2h-1 – (h-2). Here is a picture of the diagrams I drew to come up with the numbers in the table above: 
I drew as little nodes as possible on the left subtree and drew as many nodes as I could on the right subtree.
But I simply cannot figure out a pattern for the maximum possible difference between the number of nodes in the two subtrees. My current guess is that the max possible difference between the two number of nodes is 2h-1 – (h-2). Here is a picture of the diagrams I drew to come up with the numbers in the table above: I drew as little nodes as possible on the left subtree and drew as many nodes as I could on the right subtree.Asked By : user2635911
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/26100
