Minimum space needed to sort a stream of integers

Ok, it’s way past my bedtime, but this won’t let me go, so here’s a second try (deleted my first)… Before going into the specifics of how to sort the numbers, I will start by representing them not as a sequence of integers $i_1, i_2, dots , i_n$, but as a sequence of their differences, i.e. $delta_k = i_k – i_{k-1}$ where, by convention, $i_0 = 0$. Then, in order to represent these values, I will first group them into buckets depending on the number of bits needed for their representation, with the assumption that I need one bit to represent 0. Since the numbers are between 0 and 99’999’999, I will need 27 buckets. For each bucket, I will choose a prefix from the set 1, 01, 001, 0001, etc… Up to 000000000000000000000000001. Obviously, I will choose the shortest prefix for the largest bucket, the second-shortest for the second largest, etc… The sequence of $delta_k$ can then be written as pairs of prefixes and values, whereby for the values $>1$, the leading bit can be omitted. For any random set of numbers, then, how many bits do I need to represent the sequence of $delta_k$? For a constant sequence, e.g. $0, 0, 0, 0, dots , 0$, I only have to store one million representations of the number $0$, or with the above encoding, 10, hence 2 million bits. For any other constant, it would be 2 million bits plus the number of bits of that value for the initial $delta_1$. The same computation goes for an increasing sequence, e.g. $0, 1, 2, 3, dots , n$, where $delta_k=1$ and the sequence is represented as a million copies of 11. Now what is the worst-case, i.e. what sequence of $delta_k$ will give the longest sequence of bits? The worst we can do is make sure that each bucket has one entry less than the previous one, choosing the smallest $delta_k$ possible, thus assigning the largest prefix to the longest sequences. For simplicity, I’ll assume that $K$ buckets have the same amount of entries, with the shortest prefix assigned to the shortest sequence. This means that we have $n$ ones, $n$ twos, $n$ fours, etc… To represent the $j$th bucket, we need $2j-1$ bits, except for the first bucket, that needs $2$ bits. So if we put $m$ $delta_k$s into each of the $K$ buckets, we need $mleft(2 + sum_{j=2}^{K}2j-1right) = m(K^2 + 1)$ bits. However, the sum of all the $delta_k$ must not exceed 99’999’999. This sum, assuming we’ve kept the $delta_k$ as small as possible, is $msum_{j=2}^{K}2^{j-1} = m(2^K-2)$. So here’s the question: is there a combination of $K$ and $m$ such that

• $m(2^K-2) < 100’000’000$, e.g. the largest value is $<100,000,000$,
• $Km < 1’000’000$, e.g. there are at most a million values, and
• $m(K^2+1) > 8’000’000$, e.g. we use more than $8,000,000$ bits?

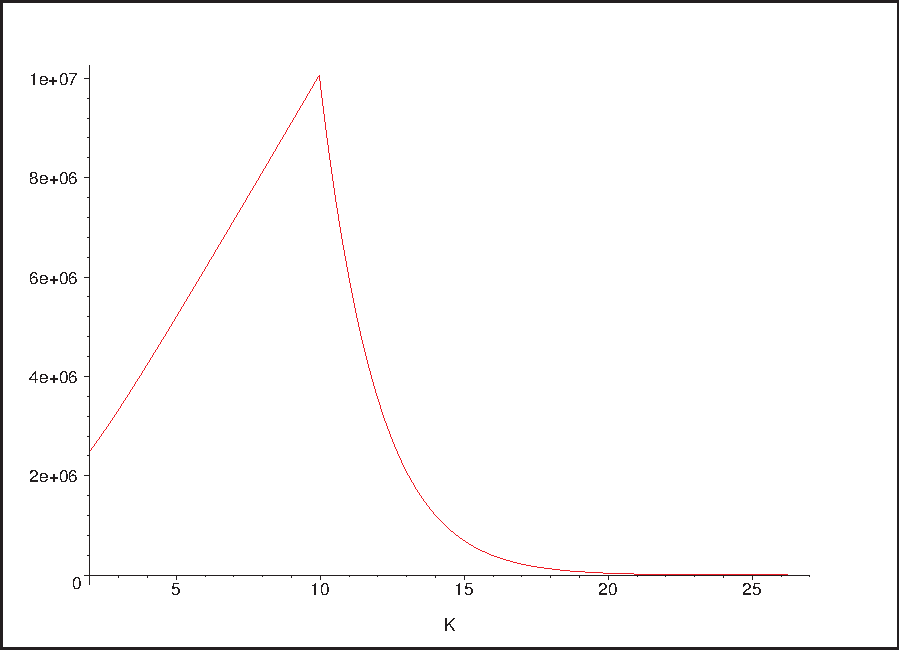
Unfortunately, this does happen. Here’s a plot of the number of bits as computed in Maple with plot( min( 100000000/(2^K-2) , 1000000/K ) * (K^2 + 1) , K=2..27 ): So we can represent any sequence of up to one million numbers in $[0,99,999,999]$ using roughly 10 million bits. This is, unfortunately, still above the specification. But how can we sort numbers like this? Well, remember that the numbers come in one by one, so as each number comes in, we update its bucket count ($mathcal O(1)$) and compute the new optimal prefixes for each bucket ($mathcal O(loglog(i_mathsf{max}))$ if the buckets are indexed in a heap). We then run through our encoded $delta_k$, reading each entry, computing the respective $i_k$ from the cumulative sum, and comparing it to the new value. If the computed $i_k$ exceeds the new value, we encode the new value and write it back, along with the adjusted $delta_k$, using the new encoding. Otherwise, we just write back the $delta_k$ with the new encoding. But write-back where? Well, if we treat our eight million bits as one large ring buffer, we can append the new, re-coded sequence of $delta_k$ to the old sequence, re-writing the old values as we go along. We’ve got almost 1 million extra bits from the worse-case scenario, and I don’t think the re-coding can cause that amount of stretching to make this not work. All in all, this leaves us with a $mathcal O(n)$ cost for inserting the $n$th number, which gives us an average-case cost of $mathcal O(N^2)$ for a total of $N$ elements. This isn’t really good, but speed did not seem to be a criteria.