Cycle Property: For any cycle C in the graph, if the weight of an edge e of C is larger than the weights of all other edges of C, then this edge cannot belong to an MST. Proof: Assume the contrary, i.e. that e belongs to an MST T1. Then deleting e will break T1 into two subtrees with the two ends of e in different subtrees. The remainder of C reconnects the subtrees, hence there is an edge f of C with ends in different subtrees, i.e., it reconnects the subtrees into a tree T2 with weight less than that of T1, because the weight of f is less than the weight of e.
Why does the proof assume that e belongs to MST? If e belongs to a cycle, and it belongs to MST, doesn’t it immediately imply that the MST has a cycle and therefore is not a tree? Please show me why I am not understanding this proof correctly. i.e. How can we have an edge e already in the tree but the tree remains acyclic? 
Asked By : Beached Whale
Answered By : snorberhuis
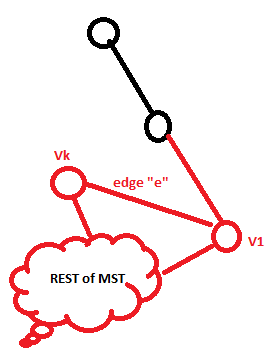
- E belongs to a cycle in the graph and to the MST.
- Not every other edge of the cycle are in the MST.
If you look at your drawing, then either one of the edges towards the rest of the MST is redundant. Because not all edges of the cycle are in the graph results in that if you remove E you get two subtrees. To answer your question about why the proof begins with assuming that e belongs to the MST: Proof by contradiction starts with assuming the opposite of what you are trying to proof. Then you reason with that assumption until you run into a contradiction. A contradiction means that your assumption must be false. If you assumption is false, then the opposite of your assumption is true. If you just look for images and MST examples there are enough examples with a cycle. Try to follow the reasoning of the proof and you will see why it is sound.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/35434