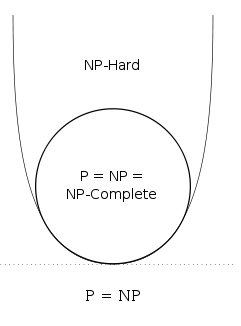
Problem Detail: As we all know the million dollar question in Computer Science P=NP or not. I was trying to understand it and got some doubts please tell me whether I’m right or wrong N=NP in two cases
Case 1: We have found an algorithm which can solve a NP-Complete problem in P-Time. This implies that P=NP=NP-Complete. But still we can not say anything about the NP-HARD Problems.
Case 2: We have found an algorithm which can solve a NP-Hard problem in P-Time. This implies that P=NP=NP-Complete=NP-Hard.
Am I right or I’m missing some point.
Asked By : Atinesh
Answered By : David Richerby
Case 1 is almost correct: if you could solve a single NP-complete problem in polynomial time, then every other NP problem can be solved by first reducing to the solved problem and then using the polytime algorithm for that. However, even if P NP, the trivial languages $emptyset$ and $Sigma^*$ are not NP-complete under many-one reductions, so NP $neq$ NP-complete. Case 2 is incorrect. NP-hard is not a complexity class, as such, and NP-hard problems can have arbitrarily high complexity. To take an extreme case, the halting problem in NP-hard but you wouldn’t be able to solve that by proving P = NP. Also, any EXP-complete problem is NP-hard, since NP $subseteq$ EXP, so any problem in NP is reducible to any EXP-complete problem. However, by the time hierarchy theorem, P $neq$ EXP so there cannot, in fact, be any polytime solution to this NP-hard problem, even if P = NP.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/21659 Ask a Question Download Related Notes/Documents
