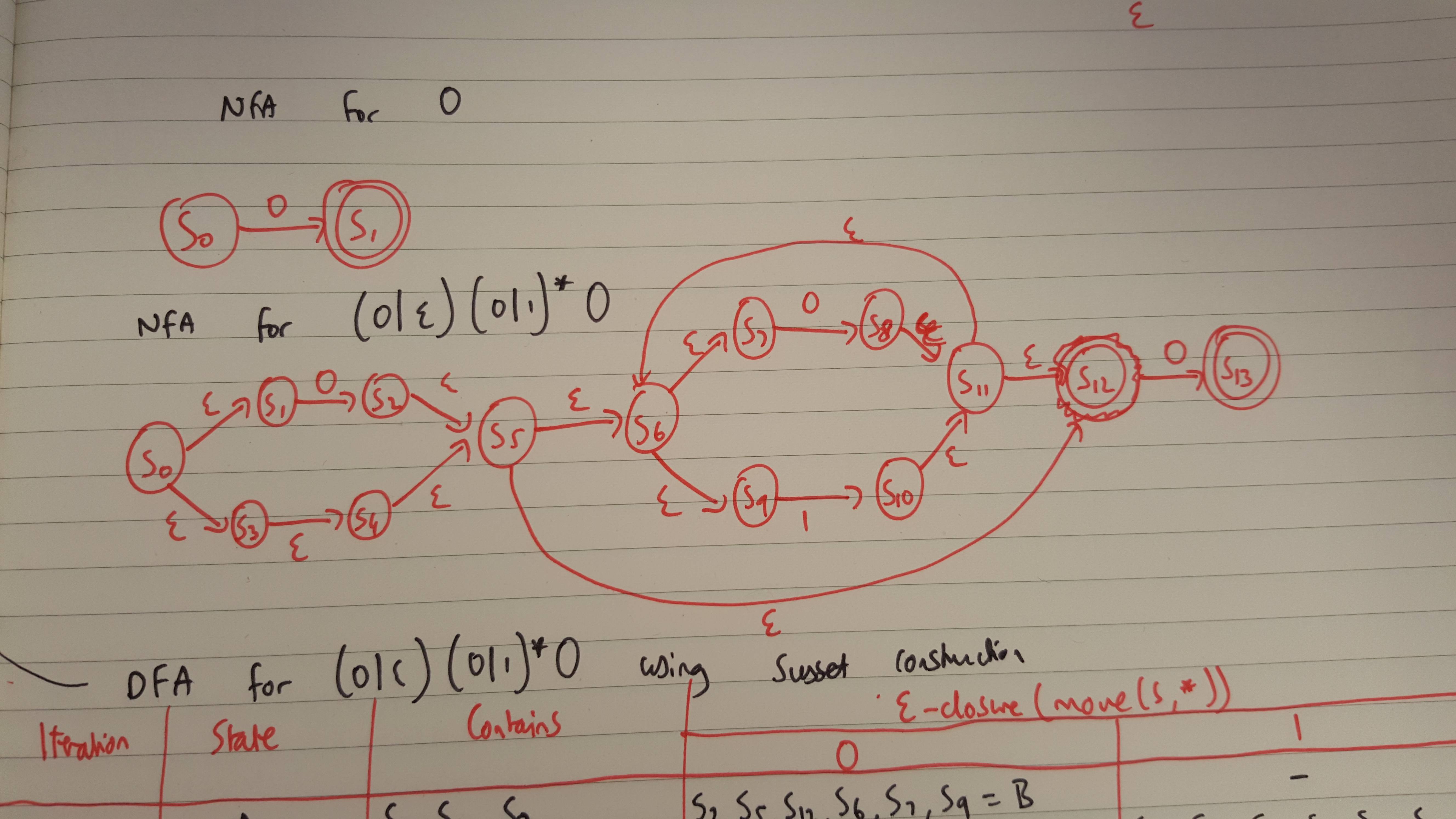
Problem Detail: I’ve been trying to convert a regular expression to a non-deterministic finite automata (NFA) first using Thompson’s construction, giving: 
, which looks correct. I am then using subset construction to create the DFA from the NFA, shown here. 
But this does not look correct to me, as for example 0 followed by 0 is not valid according to the DFA I have constructed. I was wondering how should I be modelling the epsilon in the original regular expression, as I have simply treated it as a normal epsilon.
, which looks correct. I am then using subset construction to create the DFA from the NFA, shown here. But this does not look correct to me, as for example 0 followed by 0 is not valid according to the DFA I have constructed. I was wondering how should I be modelling the epsilon in the original regular expression, as I have simply treated it as a normal epsilon.Asked By : AkshaiShah
Answered By : Renato Sanhueza
I transformed your NFA into a DFA as an exercise for my future test. $epsilon-closure{S_0}= {S_0,S_1,S_3,S_4,S_5,S_6,S_7,S_9,S_{12}}= A$ $1)$ From $A$ consuming $0$: ${S_2, S_8 ,S_{13}}$ $epsilon-closure{S_2, S_8 ,S_{13}}= {S_2,S_5,S_6,S_7,S_8,S_9,S_{11},S_{12},S_{13}}=B$ From $A$ consuming $1$: ${S_{10}}$ $epsilon-closure{S_{10}}= {S_6,S_7,S_9,S_{10},S_{11},S_{12}}=C$ $2)$ From $B$ consuming $0$: ${S_2, S_8 ,S_{13}}$ $epsilon-closure{S_2, S_8 ,S_{13}}= B$ From $B$ consuming $1$: ${S_{10}}$ $epsilon-closure{S_{10}}=C$ $3)$ From $C$ consuming $0$: ${S_8 ,S_{13}}$ $epsilon-closure{S_8 ,S_{13}}= {S_6,S_7,S_8,S_9,S_{11},S_{12},S_{13}}=D$ From $C$ consuming $1$: ${S_{10}}$ $epsilon-closure{S_{10}}= C$ $4)$ From $D$ consuming $0$: ${S_8 ,S_{13}}$ $epsilon-closure{S_8 ,S_{13}}= D$ From $D$ consuming $1$: ${S_{10}}$ $epsilon-closure{S_{10}}= C$ Then the initial state of the DFA is $A$ because it contain $S_0$. The final states of the DFA are $B$ and $D$ because they contain $S_{13}$. 
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/42176
