Problem Detail: I’m using Thompson’s algorithm to convert from a regular expression to a NFA. Is Thompson’s algorithm guaranteed to always output a minimal NFA, i.e., a NFA with the smallest possible number of states? For instance, consider this example. I have the regular expression $(a|b)$. According to this website, Thompson’s algorithm converts it to the following NFA:
o--->o /ε a ε >o O ε b /ε o--->o
However, the following NFA is smaller and seems like it would also be equivalent:
o a/ ε >o O b /ε o
Why doesn’t Thompson’s algorithm output the latter NFA? What did I miss here? Is that Thompson’s construction algorithm not optimized at all?
Asked By : nowox
Answered By : Renato Sanhueza
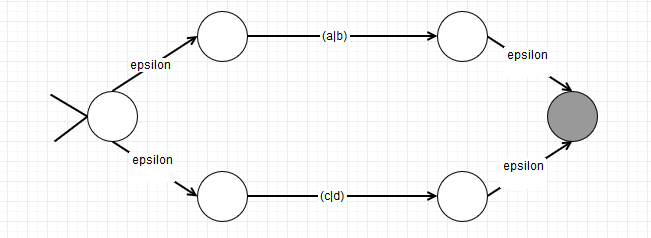
I had this same doubt when I was studying the Thompson’s construction. As I see I am not the only one I will try to solve the mistery. Consider the regular expression: $$(a|b)|(c|d)$$ With Thompson’s construction we generate first: 
and then 
Now lets use the noxwox’s construction that you suggested. First we have: 
And finally: 
Can you see the difference? I had a first suspicion watching this two results. Then I reviewed the Thompson’s constructions and I noticed something interesting. We can see the NFAs as directed graphs and the Thompson’s construction guarantee a graph whose nodes have at most two successors So here start my conclusion: Generate the data structure to store a NFA obtained by Thompson’s construction is very easy because it is a set of nodes with two pointers each. If we use nowox’s construction we don’t know a priori the numbers of successors of each node and we have to change dynamically the amount of memory reserved for each node or be inefficient in the memory management. From this point of view the Thompson’s construction algorithm guarantee a graph that is easy and fast to generate in a computer and I think that the aditional computational cost of having more states than the NFA generated by nowox’s construction is overshadowed by the backtracking mechanic of the NFAs.
and then Now lets use the noxwox’s construction that you suggested. First we have: And finally: Can you see the difference? I had a first suspicion watching this two results. Then I reviewed the Thompson’s constructions and I noticed something interesting. We can see the NFAs as directed graphs and the Thompson’s construction guarantee a graph whose nodes have at most two successors So here start my conclusion: Generate the data structure to store a NFA obtained by Thompson’s construction is very easy because it is a set of nodes with two pointers each. If we use nowox’s construction we don’t know a priori the numbers of successors of each node and we have to change dynamically the amount of memory reserved for each node or be inefficient in the memory management. From this point of view the Thompson’s construction algorithm guarantee a graph that is easy and fast to generate in a computer and I think that the aditional computational cost of having more states than the NFA generated by nowox’s construction is overshadowed by the backtracking mechanic of the NFAs.Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/43845 Ask a Question Download Related Notes/Documents
