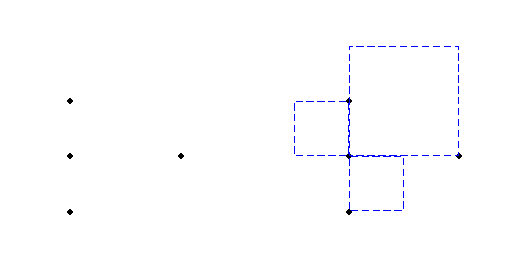
Problem Detail: I am looking for an algorithm to solve the following problem: INPUT: a set of $n$ points in the plane, $(x_1,y_1),…,(x_n,y_n)$. OUTPUT: a set of $n-1$ axis-parallel interior-disjoint squares, such that the boundary of each square contains at least two points. (*) Here is an example of input (left) and possible output (right) for $n=4$: 
Efficiency is not a concern right now – the time complexity may be exponential in $n$ (since I will usually use this algorithm with small $n$’s). My first thought was along the following lines:
Efficiency is not a concern right now – the time complexity may be exponential in $n$ (since I will usually use this algorithm with small $n$’s). My first thought was along the following lines:- For every pair of points, find a square that touches these two points.
- In the resulting set of $n(n-1)/2$ squares, find a subset with $n-1$ squares that are interior-disjoint, or report that such a set does not exist.
The problem is that, for every two points, there may be infinitely many squares that touch them. For example, the points $(0,0)$ and $(10,7)$ are touched by any square with a side-length of 10 and lower-left corner in $0 times [-3,0]$. How would you approach this problem? (*) NOTE: I don’t know whether such a set of $n-1$ squares always exists. I want to play with points in order to gain some intuition about this question and maybe find a counter-example.
Asked By : Erel Segal-Halevi
Answered By : D.W.
For a given pair of points, suppose you know which sides of the square they touch, and they are not touching the same side (of course, there are only 12 possibilities for this); fix this information about what side each is on. For example, with your example of points at $(0,0)$ and $(10,7)$, say that we’ve decided that $(0,0)$ will be on the left (west) side of the square and $(10,7)$ will be on the right (east) side of the square. It is true that there there can be infinitely many possible squares that touch those points at the given sides, as you explain in the question. However, you can always reduce this to looking at finitely many possibilities. In particular, I think it suffices to consider at most $2n$ candidate squares, out of this infinite set: the $n$ candidates whose bottom (south) side is at $y$-value $y_1$, $y_2$, …, or $y_n$, and the $n$ candidates whose top (north) side is at $y$-value $y_1$, $y_2$, …, or $y_n$. In other words, you can consider only cases where the lower-left corner is at one of the points $${(0,y_i) : i in {1,dots,n} wedge -3 le y le 0} cup {(0,y_i-10) : i in {1,dots,n} wedge -3 le y le 0}.$$ Of course, any square that contains some other point in its interior can be immediately ruled out. (I don’t have a proof of this statement; this is just what my intuition suggests.) I’m not quite sure what to do if both points are on the same side (e.g., they have the same $x$-value or the same $y$-value). Perhaps we can use a similar argument to argue that there are at most $(2n)^2$ candidate squares that must be considered, but I’m not sure. This immediately suggests an exponential-time algorithm. At each step, you non-deterministically select a pair of points that aren’t already covered by the existing set of rectangles. Now you’re going to enumerate all candidate squares that touch those two points and non-deterministically select one such square. To help with this, enumerate all 12 or 16 possibilities for which side of the square each point is on, and non-deterministically select one. Next consider the $le 2n$ candidates suggested by these possibilities, and non-deterministically select one. This gives you a square; add it to your collection, and go on to the next step. You can resolve the non-determinism using backtracking. This algorithm might work well enough to experiment with many collections of points and see if you can find a counterexample for your conjecture that it is always possible to find such a set of $n-1$ squares.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/19222 Ask a Question Download Related Notes/Documents
