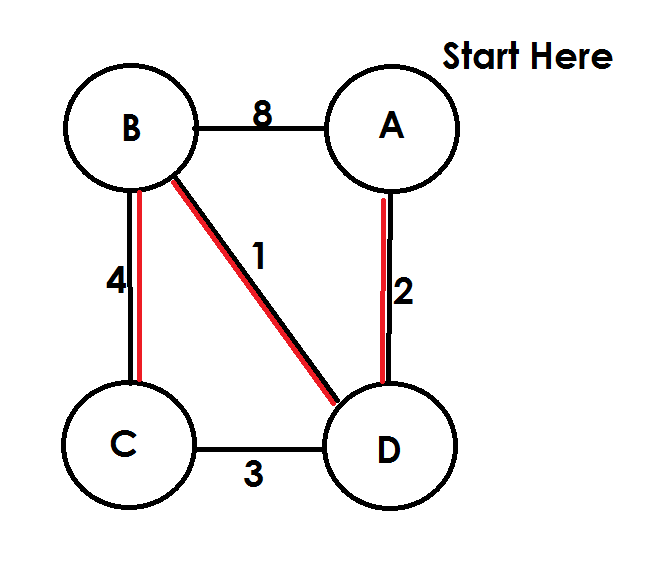
Problem Detail: I just wrote a program that runs the Travelling Salesman Problem using the Nearest Neighbor Algorithm. Afterwards, I started looking into Minimum Spanning Trees (MST). From my understanding: The Nearest Neighbor Algorithm traverses a graph starting at one vertex, and then it travels to the next vertex following the edge with the shortest distance (lightest weight) between them. An MST is a subgraph of the original graph whose vertices are all connected. The total of the edge weights in the subgraph should be as small as possible. You can use Kruskal’s algorithm to find MSTs. As I was looking at the paths taken when implementing the Nearest Neighbor Algorithm, I noticed that it could possibly sometimes return a MST. Is the Nearest Neighbor Algorithm a valid algorithm to find a Minimum Spanning Tree? It seems like it should be. It’s terribly similar to Kruskal’s algorithm (from what I have read so far). However, I never see it listed as a possible option for finding MSTs. Thanks for any help in advance. Edit for clarity: The Nearest Neighbor Algorithm is described here. From what I read, it works like so:
startVertex = vertex V for (egdes : totalEdges){ find the edge with the smallest weight connected to vertex V that has not been visited } nextVertex = vertex on the other end of the edge with the smallest weight move to nextVertex Here is an example:
Each vertex is visited and, looking at the red lines, you get an MST for that graph. 
If you do that, you get an MST. My question is, is that a valid way of getting an MST? It seems like it is since it’s so much like Kruskal’s or Prim’s algorithm.
Asked By : JustBlossom
Answered By : David Richerby
Your algorithm starts at some vertex and then always move to the closest vertex that’s not been visited so far. That’s not guaranteed to find the minimum spanning tree, as the example in your question shows. First, in a general graph, the algorithm might get stuck: you might end up at a vertex where you’ve already visited all the neighbours. For example, if you start your algorithm at $D$, it will go to $B$, then $C$ and then it’s stuck because it’s already visited both of $D$’s neighbours. The set-up of Hamiltonian cycle avoids this possibility by having an edge between every pair of vertices. Second, even if your graph contains every possible edge, the algorithm can only produce a path, so it won’t produce the minimum spanning tree in any graph where the M.S.T. isn’t a path. For example, take vertices ${1, dots, n}$ with $w(1,i)=1$ for all $i$ and $w(i,j)=2$ for all $i,jgeq 2$. The M.S.T. is all the edges from $1$, and this has weight $n-1$. But your algorithm will find some path that uses only one or two of the weight-$1$ edges, so will have weight $2n-3$ or $2n-4$.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/55019