[Solved]: Log-Space Reduction $CO-2Col le_L USTCON$

ignougroup
Problem Detail: I want to show that $CO-2Col le_L USTCON$ (Log-Space reduction)

$USTCON$

The $s-t$ connectivity problem for undirected graphs is called $USTCON$. [Input]: An undirected graph $G=(V,E)$, $s,t in V$. [Output]: 1 iff $s$ is connected to $t$ in $G$.

$CO-2Col$

A graph is $2$-colorable if there is a way to color the vertices of $G$ with $2$ colors, such that for every edge the two vertices on the edge are colored differently. $CO-2Col$ is the following problem: [Input]: An undirected graph $G$. [Output]: 1 iff $G$ is NOT $2$-colorable.

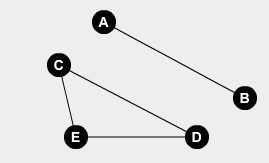
My solution is for an input graph $G$ the reduction outputs $(G’,s,t)$ where $s$ an arbitrary vertex of $G$, $t$ is one of its neighbours and $G’=G^2$ namely an edge $(u,v)in E(G’)$,iff there is $w in V (w ne u,v)$ such that $(u,w)in E(G)$ and $(w,v)in E(G)$. $G$ is bipartite iff $G’$ is not connected (and $s$ and $t$ belongs to different parts). But this only works when the input graph $G$ is connected. A counter example: (if we choose s,t to be A,B) Counter example How can I improve my reduction that it will work at the unconnected case? or maybe a new reduction is needed? Thanks!

Asked By : David

Answered By : Yuval Filmus

Hint: Extend the input graph to a connected graph which is bipartite iff the original graph is bipartite. If the original graph is not bipartite, then the new graph will a fortiori not be bipartite. The more difficult direction is ensuring that when the original is bipartite, the new edges do not render it non-bipartite. This property is satisfied as long as the edges that you introduce do not close an odd cycle. Further hint: Take $n$ copies of your original graph (where $n$ is the number of vertices), and add a new vertex $s$. Connect $s$ to the $i$th vertex in the $i$th copy.
Best Answer from StackOverflow

Question Source : http://cs.stackexchange.com/questions/22826  Ask a Question  Download Related Notes/Documents

Leave a Reply