Problem Detail: What is the maximal difference between heights of leaves in an AVL tree? I am interested only in the asymptotic difference. I am not sure about my answer – I think that it is $O(log n)$, given the fact that at every level we may have difference equal one. Am I right?
Asked By : user40545
Answered By : hengxin
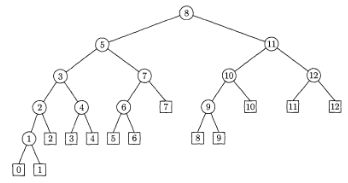
We consider Fibonacci tree ([TAOCP3, Knuth98, Sect. 6.2.1]) and compute the maximal height difference in it. A Fibonacci tree of order $k$ which is constructed recursively (see an Fibonacci tree of order 6 in the figure below; also from TAOCP):
- If $k = 0$ or $k = 1$, the tree is simply a single node.
- If $k ge 2$, the tree has a left subtree of order $k-1$ and a right subtree of order $k-2$.
It is easy to verify that a Fibonacci tree is also an AVL tree. From the figure above, we observe that the two leaves at the leftmost $l$ and at the rightmost $r$ differ most by heights ($H_l, H_r$ among all pairs of leaves. We can compute the height difference as follows. A Fibonacci tree of order $k$ has $n = F(k+2)-1 sim Phi^{k+2}$ nodes in total, where $Phi$ is the golden ratio. $$H_l – H_r = k text{ (leftmost path; decrease by 1}) – k/2 text{ (rightmost path; decrease by 2}) = k/2 text{ (maybe floor or ceiling functions here; I omit the details)}.$$ Because $n = Phi^{k+2}$, we have $k/2 = log_{Phi} sqrt{n} – 1$.
Best Answer from StackOverflow
Question Source : http://cs.stackexchange.com/questions/52077 Ask a Question Download Related Notes/Documents
