O(n*(selection+expansion+simulation+backpropagation))

Expansion just adds a child to the currently selected node. Assuming you’re not using a singly linked list or something like that to store tree children, this can happen in constant time, so we can exclude it:

O(n*(selection+simulation+backpropagation))

Given the branching factor b, and d as the depth of our tree, I’m assuming the selection phase runs in O(b*d), because at each level, the selection phase goes to all the children of the previous node. So our time complexity becomes

O(n*(b*d+simulation+backpropagation))

Backpropagation takes time proportional to the depth of the tree as well, so that becomes:

O(n*(b*d+simulation+d))

But now I’m not sure how to add the simulation phase to this. It’ll be proportional to the depth of the tree, but for each iteration, the running time depends heavily on the implementation as far as I know.

What’s monte carlo tree search

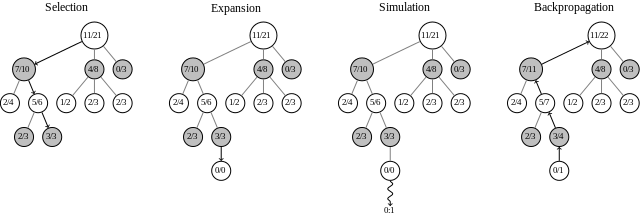
Monte Carlo Tree Search (MCTS) is a tree search algorithm that tries to find the best path down a decision tree, mostly used for game playing. In games with a high branching factor, it can often go deeper than algorithms like Minimax, even with Alpha-Beta pruning, because it only looks into nodes that look promising. For a certain number of iterations (or a certain amount of time), the algorithm goes through these four phases: Selection Starting at the root node, go down the tree until you find a node that is not fully expanded, or a leaf node. At each level, select the child that looks most promising. There are many ways of making this selection, but most implementations (including mine) use UCB1. expansion Expand the selected child by looking at one of its unexplored children. simulation Simulate a “rollout” from the newly discovered child. Again, there are many ways to do this, but many implementations just take a random child until it reaches an end node. Take note of whether the simulation resulted in a success or a failure (win or loss in the case of a game). backpropagation update the information about this node, and all nodes along the path back to the root. Most implementations store two values at each node: the number of times it was part of a selection path that lead to a success, and the total number of times it was part of a selection path. These values are used during the selection phase. After you’ve run this for as long as you can, the child node of the root that looks most promising is the action to take next.

Asked By : bigblind

Answered By : Johan

Best Answer from StackOverflow

Question Source : http://cs.stackexchange.com/questions/51726  Ask a Question  Download Related Notes/Documents