Complexity Analysis of Bubble Sorting In Bubble Sort, n-1 comparisons will be done in 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So the total number of comparisons will be (n-1)+(n-2)+(n-3)+…..+3+2+1Sum = n(n-1)/2i.e O(n2) Hence Read More …
Tag: MCS031
Determine the complexity of following sorting algorithms > Bubble Sorting
Complexity Analysis of Bubble Sorting In Bubble Sort, n-1 comparisons will be done in 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So the total number of comparisons will be (n-1)+(n-2)+(n-3)+…..+3+2+1 Sum = n(n-1)/2 i.e Read More …
Determine the complexity of following sorting algorithms > Bubble Sorting
Complexity Analysis of Bubble Sorting In Bubble Sort, n-1 comparisons will be done in 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So the total number of comparisons will be (n-1)+(n-2)+(n-3)+…..+3+2+1Sum = n(n-1)/2i.e O(n2) Hence Read More …
Determine the complexity of following sorting algorithms > Merge Sort
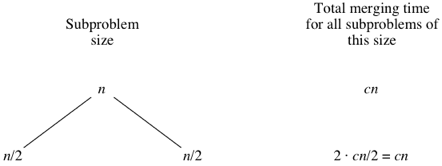
We assume that we’re sorting a total of nn elements in the entire array. The divide step takes constant time, regardless of the subarray size. After all, the divide step just computes the midpoint qq of the indices pp and rr. Recall that in big-Θ notation, we Read More …
Determine the complexity of following sorting algorithms > Merge Sort
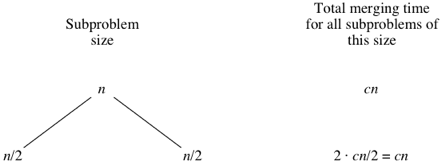
We assume that we’re sorting a total of nn elements in the entire array. The divide step takes constant time, regardless of the subarray size. After all, the divide step just computes the midpoint qq of the indices pp and rr. Recall that in big-Θ notation, we Read More …
Determine the complexity of following sorting algorithms > Merge Sort
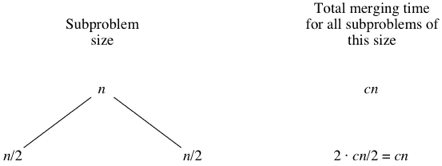
We assume that we’re sorting a total of nn elements in the entire array. The divide step takes constant time, regardless of the subarray size. After all, the divide step just computes the midpoint qq of the indices pp and rr. Recall that in big-Θ notation, we Read More …
Determine the complexity of following sorting algorithms > Quick sort
Determine the complexity of following sorting algorithms (i) Quick sort(ii) Merge sort (iii) Bubble sort (iv) Heap sort
Determine the complexity of following sorting algorithms > Quick sort
Determine the complexity of following sorting algorithms (i) Quick sort(ii) Merge sort (iii) Bubble sort (iv) Heap sort
Determine the complexity of following sorting algorithms > Quick sort
Determine the complexity of following sorting algorithms (i) Quick sort(ii) Merge sort (iii) Bubble sort (iv) Heap sort
Write Strassen’s Algorithm ? What are the limitation of Strassen’s Algorithim. Apply Strassen’s Algorithm to multiply two matrices A1 & A2 given below.

In linear algebra, the Strassen algorithm, named after Volker Strassen, is an algorithm for matrix multiplication. It is faster than the standard matrix multiplication algorithm and is useful in practice for large matrices, but would be slower than the fastest Read More …